先日公開したArduino UNO R4 Minimaの紹介記事にて、Arduinoの計算能力の比較を行いました。まだ読んでいない方はそちらの記事もどうぞ。
今回の記事では、その中で行ったArduino Uno新旧モデルの計算能力のベンチマークについてさらに詳しく解説します。実際に使用したプログラムも公開しますので、皆さんも試してみてください。

概要
今回マイコンの計算能力を比較する指標として、Arduino Uno R3(以下”R3″)とArduino Uno R4 Minima(以下”R4″)で同一のソースコードを実行して、それぞれの実行に要した時間をマイコン上のクロックで計測し、比較しました。
試験内容は以下の3点です。
- フィボナッチ数列生成
- 素数判定
- 三角関数
それぞれ、整数の加算、整数の除算、浮動小数点計算について比較することを目的としています。
ベンチマーク
ベンチマーク試験の結果は以下の通りです。それぞれ比較しやすい数値になるように計算回数を調整しています。
フィボナッチ数列生成
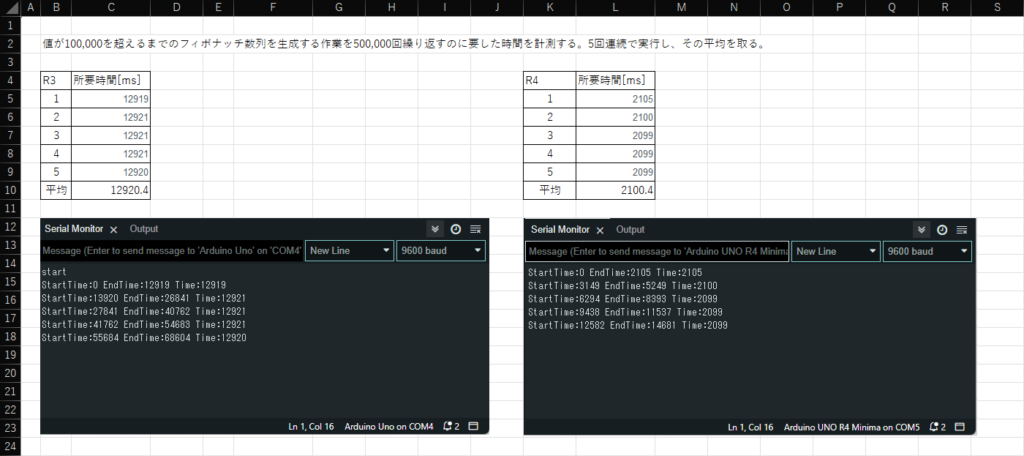
フィボナッチ数列生成では、値が100,000を超えるまでのフィボナッチ数列の生成を500,000回繰り返すのに要した時間を計測しました。その処理の5回分の結果の平均を取っています。
その結果は次の通りです。
| Arduino UNO R3 | Arduino UNO R4 Minima |
|---|---|
| 12.9[s] | 2.1[s] |
約6倍強の差があります。
動作クロックの差は3倍程度なので、それ以上に差が出た要因としては、それぞれ8bitと32bitのCPUで32bitのlong型を扱うため要する処理時間の違いなどが考えられます。これについては後述します。
素数判定
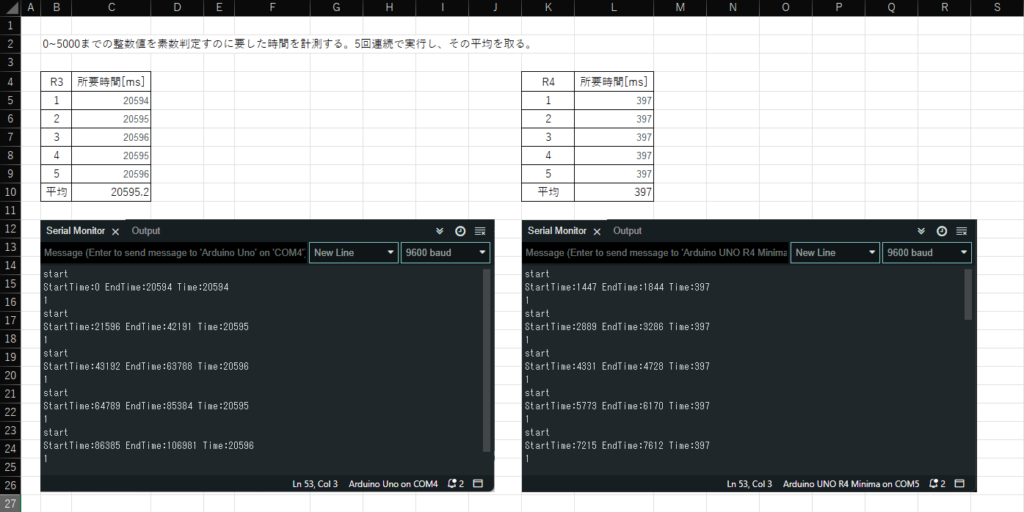
素数判定では0~50,000までの整数を素数かどうか判定するまでの時間を比較しました。
| Arduino UNO R3 | Arduino UNO R4 Minima |
|---|---|
| 20.6[s] | 0.4[s] |
結果はR4の方が圧倒的に早く、なんと50倍以上の差が出ました。
これは素数判定を行うアルゴリズムに原因があると考えられます。
多くのコンピュータは除算(割り算)を苦手としています。デジタルのCPUで除算をするために、減算(引き算)を繰り返すことでその処理を実現しているので、一つの命令で済む加算・減算に比べて、計算完了までに多くの処理が必要になるためです。
そのため、一般的にソースコードを機械語に翻訳するコンパイラは除算するソースコードを与えられたときに、ビット演算などを利用して可能な限り時間のかかる減算の繰り返し処理を回避しようとします。
そこで、あらゆる数で除算を繰り返すような処理を伴う素数判定の処理をさせてみることが本試験の目的でした。
この試験は、いかに時間のかかる処理を回避するかというコンパイラの性能の比較という意味合いもありました。
三角関数
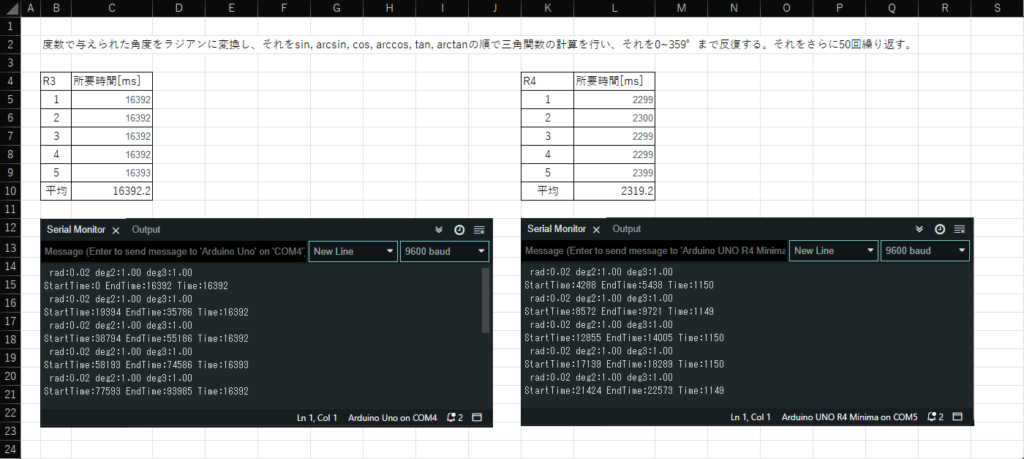
三角関数の計算として、度数で与えられた角度をラジアンに変換し、それについてsin,arcsin,cos,arccos,tan,arctanの順で計算。その角度を0~359°まで反復。さらにこれを50回繰り返すまでの時間を計測しました。
| Arduino UNO R3 | Arduino UNO R4 Minima |
|---|---|
| 16.4[s] | 2.3[s] |
本試験では7倍程度の差がでました。
これは素数判定ほどの差は出ていないようですが、やはりR4の方が高速に計算できています。
計算に用いた変数のfloat型も32bitの浮動小数点型変数です。
所感
CPUのクロック向上やSRAM拡大なども計算速度向上の要因の一つですが、特にCPUのビット数増加が効いているような印象を受けました。
R3のCPUは8bitだったため、一つのレジスタで一度に扱える数の上限は、符号付きの場合-127~127の範囲でした。それより大きい数、例えばR3でのint型のサイズである16bitの値を扱おうとした場合、下位8bitの計算、繰り上がり処理、上位8bitの計算というように、値を2進数表記した状態での桁数を扱えるbit数ごとに区切って計算する必要があるため、処理が遅くなります。
そのため、その変数が取り得る値の範囲に適した型の変数を使う必要があります。
R4ではCPUが刷新されて32bitになったことで、一度に扱える数の幅が圧倒的に大きくなりました。
そのため、32bit整数型のlong型変数はもとより、同じ32bitの幅を持った浮動小数点のfloat型の計算においても、その値を分割無しに丸ごとレジスタにコピーすることができるようになり、処理時間短縮の恩恵を受けることができるようになりました。
ただし、紹介記事でも述べたとおりR3とR4でCPUアーキテクチャが異なるため当然コンパイラも別物であり、同一のソースコードを使用してもコンパイラから出力される機械語の挙動が同一でない可能性もあるという点に留意する必要があります。
本記事の試験結果はあくまで参考値程度に考えてください。
Arduinoでは、C言語ライクなソースコード上でアセンブラを記述することができます。それを利用して、機械語レベルで全く同じ動きをするプログラムを作成して計算能力を測定することで、もっと正確なベンチマークも可能になるはずです。
いずれ機会があればやってみようと思います。
さて、Arduino Unoシリーズ新旧モデルのベンチマーク比較はいかがだったでしょうか。
正直なところ一般的な趣味レベルのマイコン工作ではR3でも「計算速度が遅い」ということはあまり無いかと思います。例えばR3でPID制御を行うとして、一般的に実用上問題ない100Hz程度の周期で浮動小数点計算を行ったとしても全く問題なく動作するはずです。それよりも2kBしかないSRAMの容量不足に悩まされることが多かったでしょうか。
今回実験で取り上げた計算速度の向上は、Arduino Unoのおよそ10年ぶりのモデルチェンジの内容の一端でしかありません。これ以外にも多くの部分に改良が施され、性能が上がっています。
それに加えて価格も安価になっているとなれば、入門機としてはベストな選択かと思います。
皆さんも是非、手に取って確かめてみてください。
さて、ベンチマークとその結果については以上になりますが、次の章ではベンチマークに使用したソースコードについて解説します。もしご興味のある方はもう少しお付き合いください。
付録:実験に用いたソースコード(むしろここからが本題)
フィボナッチ数列(整数計算)
以下のプログラムを5回連続で計測し、その平均を取る。
//値が100,000を超えるまでのフィボナッチ数列を生成する作業を500,000回繰り返すのに要した時間を計測する。
#define DEBUG 0
void setup() {
Serial.begin(9600);
}
void loop() {
unsigned long x;
unsigned long prevx;
unsigned long temp;
unsigned long start_time, end_time;
unsigned long time;
start_time = millis();
for (unsigned long a = 0; a < 500000; a++) {
x = 1;
prevx = 0;
while (x < 100000) {
temp = x;
x = prevx + x;
prevx = temp;
#if DEBUG
Serial.println(x);
#endif
}
}
end_time = millis();
time = end_time - start_time;
Serial.print("StartTime:");
Serial.print(start_time);
Serial.print(" EndTime:");
Serial.print(end_time);
Serial.print(" Time:");
Serial.println(time);
delay(1000); //1秒待機
}スケッチの解説
Arduinoを触ったことがある方はご存じかと思いますが、Arduinoのソースコードには必ず二つの関数があります。setup()とloop()です。
プログラムが実行されると、まず最初にsetupの内容が一度だけ実行され、それ以降はloopの内容が繰り返し実行されます。
setup内では、起動時に必要な処理を行います。
本プログラム内ではSerial.begin(9600);でPCへのシリアル通信のビットレートの設定を行い、通信を確立します。
loop内ではセンサの状態を監視して何かの処理を行ったり、条件分岐により別の関数を呼ぶなどの処理を記述するのが一般的です。
デジタル入力を使用した割込み処理については、今回は割愛します。
プログラムの先頭の#define DEBUG 0はデバッグ用のマクロの定義です。詳細は後述します。
unsigned long x;
unsigned long prevx;
unsigned long temp;
unsigned long start_time, end_time;
unsigned long time;
start_time = millis();まずloop関数冒頭のこの部分についてです。
loop関数内で使用する変数を定義しています。変数にはスコープがありますので、loop関数内からしかこれらの変数を読み書きすることはできません。
xは計算したフィボナッチ数列の最後の要素、prevxは最後から2番目の要素、tempは計算用の一時変数を表します。また、start_time、end_timeは後述の方法で測定開始と測定終了の時刻を記録し、その差から計算にかかった時間を算出し、timeに代入します。
loop関数内で定義された変数は明示的にstaticで宣言しない限り、loop関数の先頭に戻るごとにリセットされてしまいますが、今回の試験では特に問題ありません。
for (unsigned long a = 0; a < 500000; a++) {
x = 1;
prevx = 0;
while (x < 100000) {
temp = x;
x = prevx + x;
prevx = temp;
#if DEBUG
Serial.println(x);
#endif
}
}これはフィボナッチ数列の計算部分です。
現在の項とひとつ前の項を表す変数に1,0を代入し、そこから要素が閾値を超えるまで数列を計算します。
それをさらにfor文で規定回数繰り返すことで処理が完了します。要素二つの変数はfor文の先頭で代入しています。temp = x;で現在の項を一時変数に退避し、x = prevx + x;で次の項を計算して現在の項に代入、prevx = temp;で一時変数に退避しておいた現在の項を一つ前の項として代入します。
これをwhile文の中で最後の項の値が条件式に一致している間だけ繰り返し、計算します。
#if DEBUG~#endifのディレクティブで囲まれた部分は、先ほどのデバッグ用プリプロセッサに関わってくる部分です。C系言語における#から始まる記述はプリプロセッサと呼ばれ、コンパイル段階で代入、置換、条件分岐などの処理が行われます。
この場合デバッグ用マクロ(変数のようなもの)DEBUGを0と定義しているので、ソースコード内の”DEBUG”はコンパイル前の段階で”0″に置換されます。そのため、#if DEBUG の条件分岐はコンパイル段階で偽と判断され、無視されることになります。すなわち、実際に実行するプログラムにこの部分の記述に対応する機械語が一切含まれないということです。一方でDEBUGを1と定義した場合、条件分岐は真となるので、デバッグ用の表示に関する命令がコンパイル処理に含まれるようになります。今回のように、厳密に実行時間を計測するために余計な処理をコンパイル結果に含めたくない場合や、大規模な処理をデバッグ等の目的で外したい場合などに有効なテクニックです。
end_time = millis();
time = end_time - start_time;
Serial.print("StartTime:");
Serial.print(start_time);
Serial.print(" EndTime:");
Serial.print(end_time);
Serial.print(" Time:");
Serial.println(time);
delay(1000); //1秒待機計算が終わったらend_time = millis(); で終了時点の時間を取得し、time = end_time - start_time;でtime変数にループ開始時点の時刻との差分を取っています。
millis()関数は、マイコン電源投入からの経過時間をミリ秒で返してきます。そのため変数がオーバーフローしてしまうと時間の差が正確に取得できなくなりますが、戻り値の型はunsigned longで0~2^32-1 = 4,294,967,295の値を取ることができます。そのため、およそ50日間はその心配はありません。
マイクロ秒単位の時間を取得できるmisros()という関数もありますが、こちらは71分ほどでオーバーフローします。
最後のSerial.printで始まる部分は、シリアル通信でPC側に計測結果を送信する部分です。
なお、この時間計測~結果出力の部分については後で出てくるスケッチでも概ね共通となっています。
素数判定
以下の5回連続で実行し、その平均を取る。
//0~50000までの整数値を素数判定するのに要した時間を計測する。
#define DEBUG 0
void setup() {
Serial.begin(9600);
}
bool isPrime(unsigned long n) {
// 2未満の数は素数ではない
if (n <= 1) {
return false;
}
// 2は素数
if (n == 2) {
return true;
}
// 偶数は素数ではない
if (n % 2 == 0) {
return false;
}
// nを2からsqrt(n)までの数で割ってみて、割り切れるかどうかを確認
// 割り切れる場合、素数ではない
for (int i = 3; i * i <= n; i += 2) {
if (n % i == 0) {
return false;
}
}
// それ以外の場合、素数である
return true;
}
void loop() {
unsigned long start_time, end_time;
unsigned long time;
bool result;
Serial.println("start");
start_time = millis();
for(unsigned long x=0;x<50000;x++){
result=isPrime(x);
#if DEBUG
Serial.print(x);
Serial.print("\t");
Serial.println(result);
#endif
}
end_time = millis();
time = end_time - start_time;
Serial.print("StartTime:");
Serial.print(start_time);
Serial.print(" EndTime:");
Serial.print(end_time);
Serial.print(" Time:");
Serial.println(time);
Serial.println(result);
delay(1000);//1秒待機
}スケッチの解説
for(unsigned long x=0;x<50000;x++){
result=isPrime(x);
#if DEBUG
Serial.print(x);
Serial.print("\t");
Serial.println(result);
#endif
}loop関数の中は先ほどのフィボナッチ数列生成とほぼ同じです。閾値を超えるまでの数値を順に素数判定関数に渡すループがあり、その後に結果を表示するまでの処理をloop関数そのもので回しています。
bool isPrime(unsigned long n) {
// 2未満の数は素数ではない
if (n <= 1) {
return false;
}
// 2は素数
if (n == 2) {
return true;
}
// 偶数は素数ではない
if (n % 2 == 0) {
return false;
}
// nを2からsqrt(n)までの数で割ってみて、割り切れるかどうかを確認
// 割り切れる場合、素数ではない
for (int i = 3; i * i <= n; i += 2) {
if (n % i == 0) {
return false;
}
}
// それ以外の場合、素数である
return true;
}素数判定関数です。
このプログラムを作った目的は、先ほども述べたとおり、マイコンに除算を大量にさせることで負荷をかけ、ベンチマークを行うことでした。
判定の高速化のために0,1や2の倍数を最初に弾く処理が入っていますが、ベンチマークという観点から見れば不要な処理でした。
そもそも引数として渡される値がunsigned longなので、0,1を除外するだけでよいでしょう。
for (int i = 3; i * i <= n; i += 2)の部分で素数の定義は「1とその数自身との外には約数がない正の整数」なので、先ほど除外した3以降から対象の数nの平方根までを、偶数を飛ばすために2個おきにforループで回し、if (n % i == 0)で除算余数が0であるか(割り切れるか)を計算することで素数であるかを判定します。
もし判定対象nが合成数であった場合、1以外の約数2つの積としてn = a*b (1<a≦b, a,b∈Z)で表せます。1<a≤bより、n = a*b ≧ a*a = a^2であり、したがってa ≦ sqrt(n)が導けます。
これにより、探索をsqrt(n)で打ち切ることで、素数判定を高速に行うことができるのですが、やはりこれについてもベンチマークという意味であれば3~nまで1ずつ探索を行った方がよかったかもしれません。
三角関数
以下のプログラムを50回繰り返し、その平均を取る。
//度数で与えられた角度を弧度法に変換し、それをsin, arcsin, cos, arccos, tan, arctanの順で三角関数の計算を行い、それを0~359°まで反復する。
void setup() {
Serial.begin(9600);
}
float deg_to_rad(float deg) {
float rad;
rad = deg * (PI / 180);
return rad;
}
float rad_to_deg(float rad) {
float deg;
deg = rad / (PI / 180);
return deg;
}
void loop() {
unsigned long start_time, end_time;
unsigned long time;
float rad, deg1, deg2, deg3;
unsigned int temp;
start_time = millis();
for (int x = 0; x < 50; x++) {
for (int deg = 0; deg < 360; deg++) {
rad = deg_to_rad((float)deg);
deg1 = rad_to_deg(asin(sin(rad)));
rad = deg_to_rad((float)deg1);
deg2 = rad_to_deg(acos(cos(rad)));
rad = deg_to_rad((float)deg2);
deg3 = rad_to_deg(atan(tan(rad)));
}
}
end_time = millis();
time = end_time - start_time;
Serial.print(" rad:");
Serial.print(rad);
Serial.print(" deg2:");
Serial.print(deg2);
Serial.print(" deg3:");
Serial.print(deg3);
Serial.print("\n");
Serial.print("StartTime:");
Serial.print(start_time);
Serial.print(" EndTime:");
Serial.print(end_time);
Serial.print(" Time:");
Serial.println(time);
delay(3000);
}コードの解説
float deg_to_rad(float deg) {
float rad;
rad = deg * (PI / 180);
return rad;
}
float rad_to_deg(float rad) {
float deg;
deg = rad / (PI / 180);
return deg;
}以上の2つの関数は、度数法と弧度法を相互に変換するための関数です。
度数degもfloatで渡す必要があります。
for (int x = 0; x < 50; x++) {
for (int deg = 0; deg < 360; deg++) {
rad = deg_to_rad((float)deg);
deg1 = rad_to_deg(asin(sin(rad)));
rad = deg_to_rad((float)deg1);
deg2 = rad_to_deg(acos(cos(rad)));
rad = deg_to_rad((float)deg2);
deg3 = rad_to_deg(atan(tan(rad)));
}
}これは主要計算部分です。
計算内容に特に意味はなく、ただむやみやたらに浮動小数点計算をさせて負荷をかけることが目的でした。
rad = deg_to_rad((float)deg);でfloat型にキャストした度数をラジアンに変換。deg1 = rad_to_deg(asin(sin(rad)));では、そのラジアンを元にsin、さらにそこからarcsinを求め、その出力のラジアンを度数に変換しています。
その後、同様にcosとarccos、tanとarctanを計算しています。
余談になりますが、本ベンチマークの実行結果の画像をご覧いただくとわかる通り、シリアルに計算途中や計算結果の角度を出力して表示しています。
これには理由があって、当初は結果出力無しでのプログラムを作成して使用していたのですが、R4だけ計算内容やループ回数に関わらず4ms程度で処理が完了してしまうという不可解な挙動を見せていたことがありました。
これは、計算結果を収める変数がプログラム内で代入されるだけで一度も呼び出されないために、コンパイラに最初から無いものとして扱われてしまったことが原因でした。
そのため、時間の計測が終了してから一度だけ読み出してやることで、コンパイラによる”無視”を回避しています。
さいごに
今回はマイコンに計算をさせ、その所要時間で計算能力のベンチマークを行うという企画でした。
除算や浮動小数点計算など、それぞれの計算種別ごとに性能を引き出せるソースコードを使用していたことがお分かり頂けたかと思います。
比較対照実験としては大成功だと思います。
今回の企画で使用したArduino UNO R4 Minimaは以下から購入できます。今回行ったテストなどぜひ皆さんも真似してみて下さい。R4 Wifiもあります。
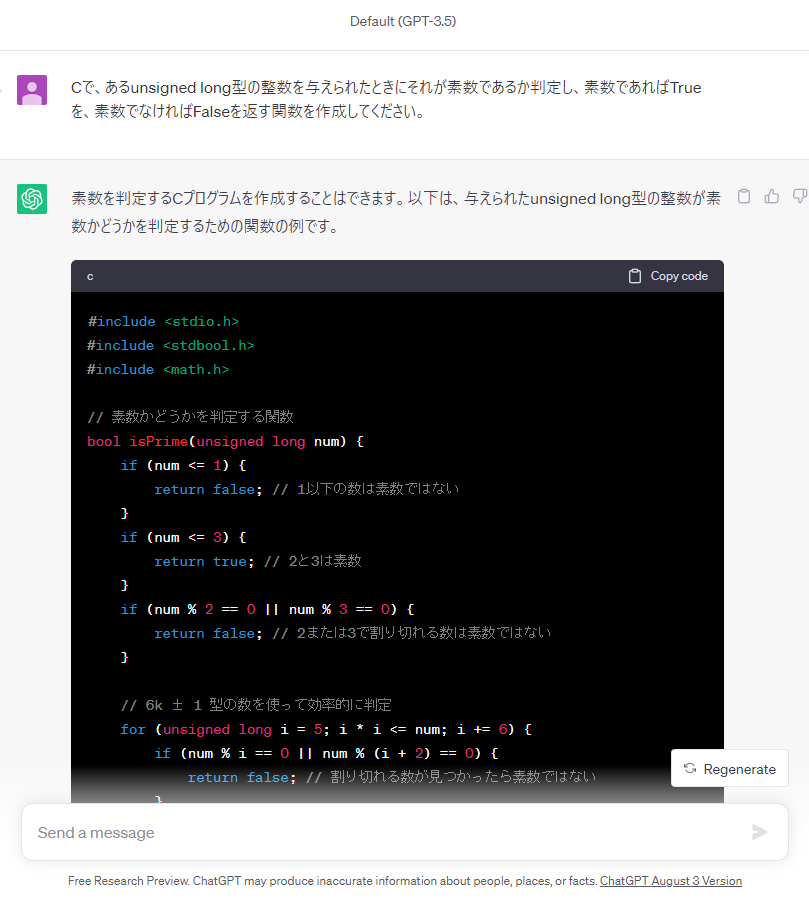
ところで、今回使用したプログラムの作成にはChatGPTの力を借りていました。
皆さんはプログラミングでChatGPTを使ったことがありますか?
入力と出力の仕様が明確になっている関数を書きたいときは、ChatGPTにお任せするのも一つの手です。ぜひ参考にしてみてください。













コメント