オペアンプを使ったアナログコンピュータを自作する【前編】

2023-10-02

今回はアナログコンピュータを作ります。

アナログコンピュータとは、デジタルではない無段階に可変する物理量を用いて計算を行う装置のことです。一般的には電子回路の電圧・電流を積分して計算を行う電子式のアナログ計算機や、摩擦や歯車の減速比などの機械的な要素を使った機械式のアナログ計算機があります｡

今回は電子回路を用いて物理現象を電圧波形として再現するアナログコンピュータを製作します。

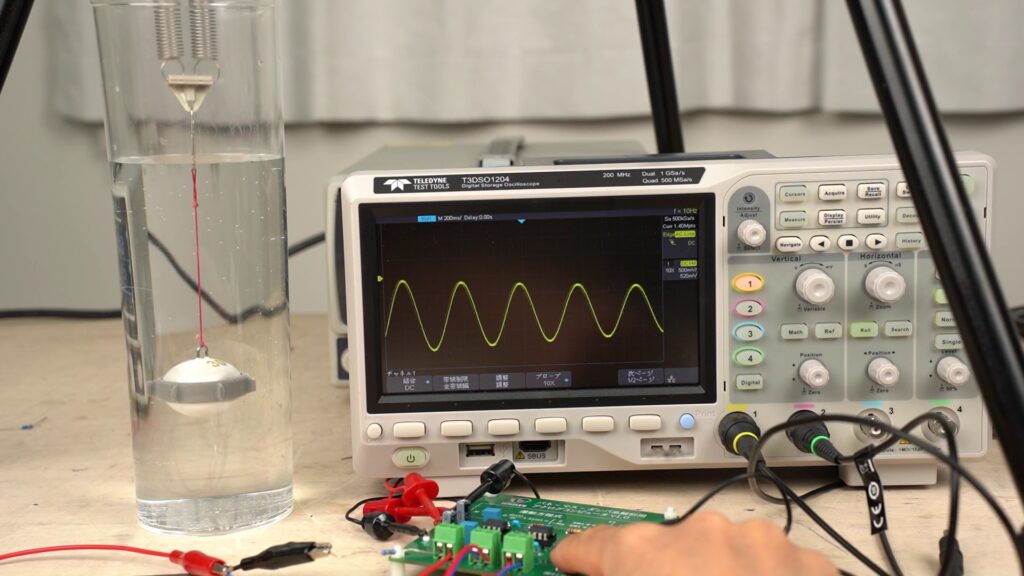
アナログコンピュータが登場した頃は、現在使われているような高速なデジタルコンピュータが存在しませんでした。複雑な連立方程式や定数を変更しながら計算を行う必要がある状況で、比較的高速に計算を行うためにアナログコンピュータというものが発達したという背景があります。

現代では半導体の登場や進化とともに、普段皆さんが使っているようなデジタル計算機が出てきたため、アナログコンピュータを見かけることはありません。

回路を用いた計算の基本

今回はバネ – マス – ダンパモデル用の、電子式のアナログ計算機を作るのが目標ですが、その前にオペアンプを用いたアナログ回路での基本的な計算の仕方から紹介していきます。

回路の説明と動作の様子

まずは簡単な計算をしてみます、足し算からです。

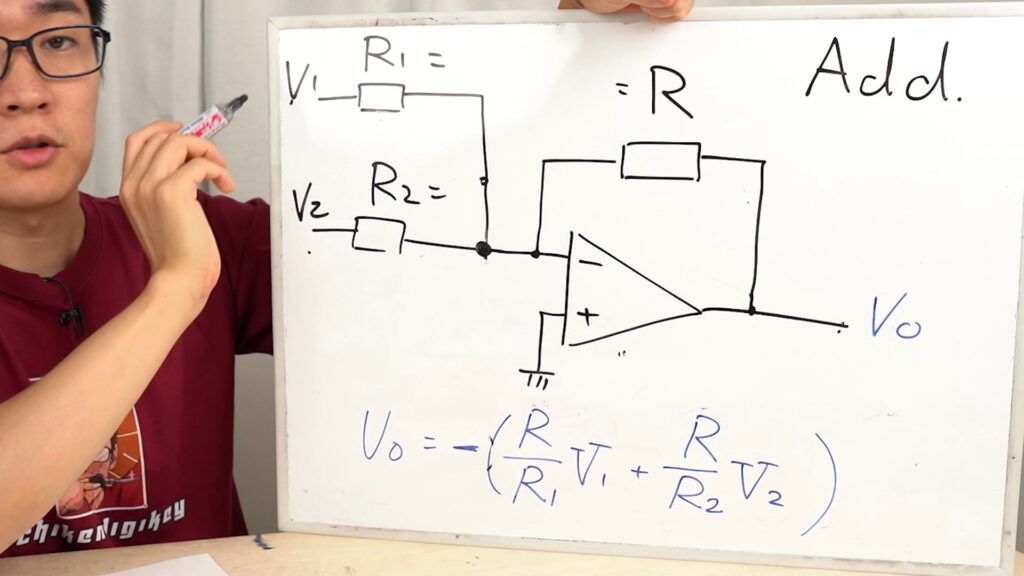
足し算の計算はこの回路で行います。V1とV2の入力を足して反転されたものがVoとして出てきます。
R1, R2に流れる電流をそれぞれI1, I2とすると、それらは次のように表すことができます。

$$I_1 = \frac{V_1}{R_2}, I_2 = \frac{V_2}{R_2}$$

この回路においてオペアンプは、負帰還によりマイナス入力端子の電圧が仮想短絡しているプラス入力端子と同じ0Vになるように電圧を出力します。

このとき、オペアンプのマイナス入力端子周辺に注目すると、キルヒホッフの法則より回路中のある1点において流れ込む電流の和と流れ出る電流の和は常に等しくなります。
（参考：電気回路の計算？？これを使います【イチケン電子基礎シリーズ】キルヒホッフの法則）

オペアンプの入力端子が吸い込む電流は無視できるレベルで小さいので、以上の式にこれを当てはめることでRに流れる電流(I)を

\begin{eqnarray}
I &=& -(I_1+I_2) \\
&=& -( \frac{V_1}{R_2} + \frac{V_2}{R_2} )
\end{eqnarray}

と表すことができます。すなわち、電流で足し算を行っているということです。
Rの抵抗値と、そこに流れる電流より、出力Voは次のようになります。

\begin{eqnarray}
V_o &=& IR \\
&=& -(\frac{V_1}{R_2} + \frac{V_2}{R_2})R \\
&=& -(\frac{R}{R_1}V_1 + \frac{R}{R_2} V_2) \\
\end{eqnarray}

ここでR1, R2, Rを同じ抵抗値とすると、先ほどの式は以下のように単純化できます。

$$V_o = -(V_1 + V_2)$$

この回路で加算が実現できるのか実験しました。R1, R2, Rはすべて同じ抵抗値です。

画像の状態ではV1に+5[V]を、V2に-3[V]を入力しています。出力電圧が-2[V]であることから、V1, V2を加算しマイナス符号をつけた値が確かに出力されていることがわかります。

引き算

足し算が出来ましたが、同じようにオペアンプを使った回路で引き算の回路も作成することができます。

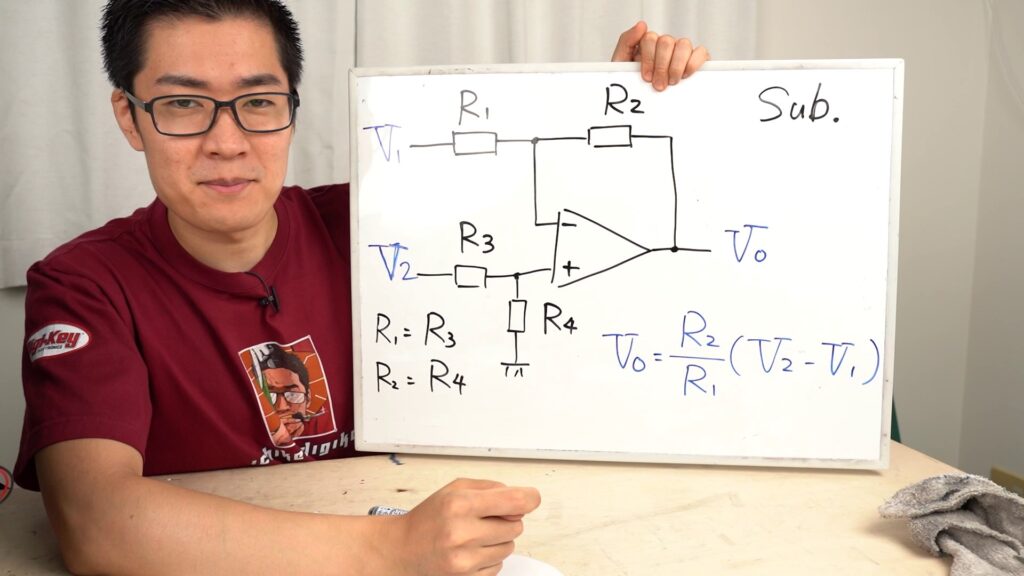
この回路の場合、VoにはV1とV2の電圧が引き算されたものがR1とR2の比率で出力されるようになります。

なお、純粋な引き算の計算を行うためには少々条件があり、オペアンプのそれぞれの入力に繋がっている抵抗値R1とR3、そしてR2とR4は同じである必要があります。この回路も先述の加算回路同様に負帰還回路ですが、基準電圧となるプラス入力端子をGNDに落とすのではなく、抵抗で分圧した電圧を入力している点がポイントです。

まず、オペアンプの入力端子にかかる電圧はV2の分圧であり、かつ、R1=R3, R2=R4なので、次のように表されます。

$$V_{in} =V_2\frac{R_2}{R_1+R_2}$$

また、この回路の負帰還回路部分の電圧は次のように表されます

$$V_o-V_{in}=\frac{R_2}{R_1}(V_{in}-V_1)$$

ここに先ほどの入力電圧を代入し、式を変形することで、減算回路の式が導出されます。

\begin{eqnarray}
V_o- V_2\frac{R_2}{R_1+R_2} &=& \frac{R_2}{R_1}(V_2\frac{R_2}{R_1+R_2}-V_1) \\\\
V_o &=& (\frac{R_2}{R_1}+1)V_2\frac{R_2}{R_1+R_2}-V_1\frac{R_2}{R_1}\\
&=& \frac{R_2+R_1}{R_1}\cdot V_2\frac{R_2}{R_1+R_2}-V_1\frac{R_2}{R_1}\\
&=& V_2\frac{R_2}{R_1}-V_1\frac{R_2}{R_1}\\
&=&\frac{R_2}{R_1}(V_2-V_1)
\end{eqnarray}

乗算除算は専用ICがある

また、乗算や除算も出来るのですが、どうしても回路が複雑になりがちで作ることが困難です。

ですのでICの状態で既に専用の乗算機や除算機というものが販売されていますので、どうしても計算を行いたいという場合にはこれらを試してみるのが良いかもしれません。今回の記事では詳細な解説は割愛します。

アナログ乗算器や除算器は、2つ以上の独立した入力電圧または入力電流の積に比例した出力電圧または出力電流を生成するデバイスです。乗算器は、乗算と除算に加えて二乗、平方根、変調関数などの演算を行うことができます。アプリケーションには、リアルタイム応答が求められるレーダー、通信、工業用制御などが含まれます。アナログ・デバイセズは、最も豊富な乗算器／除算器モデルを用意しています。
アナログ・デバイセズ : https://www.analog.com/jp/product-category/analog-multipliers-dividers.html

微積分について

さて、実際のアナログコンピュータでは微分方程式を解くことが多いかと思います。
そこで重要になってくるのが積分回路です。

積分回路

これが積分回路です。$V_{\text{in}}$の入力に対して$V_{\text{out}}(t) = -\frac{1}{R \cdot C} \int V_{\text{in}}(t) \, dt $の電圧を出力します。

今回の実験では、簡単のため1[MΩ]の抵抗と1[μF]のコンデンサの組み合わせで時定数を1として、入力電圧としてVin=1[V]を入力しています。

以上の条件から、出力電圧の式は次のように求められます。

\begin{eqnarray}
V_o &=& -\frac{1}{R \cdot C} \int V_{\text{in}}(t) \, dt\\
&=& -\frac{1}{10^3 \cdot 10^{-3}} \int V_{\text{in}}(t) \, dt\\
&=& -\int V_{\text{in}}(t) \, dt\\
&=& -t
\end{eqnarray}

実際に回路を作成して、電圧を入力した際の入力と出力の電圧の波形が以下の画像です。
1[V]の電圧を入力すると1[V/s]の割合で出力電圧が低下していることがわかります。

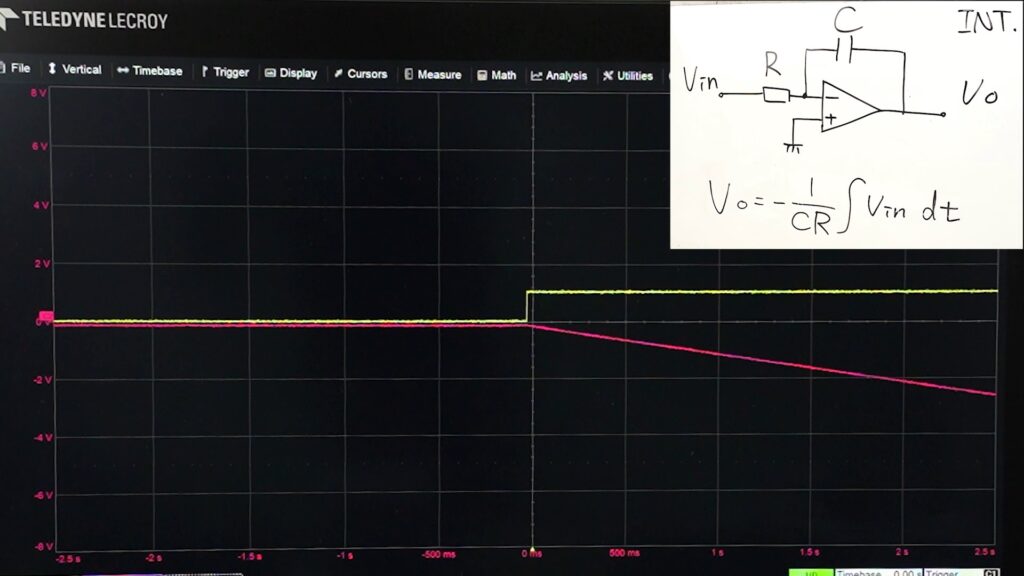
入力電圧を変動させれば、それに対応した積分結果の電圧を出力します。

微分回路

積分があるなら微分もアナログコンピュータで実現できます。以下の回路を使います。

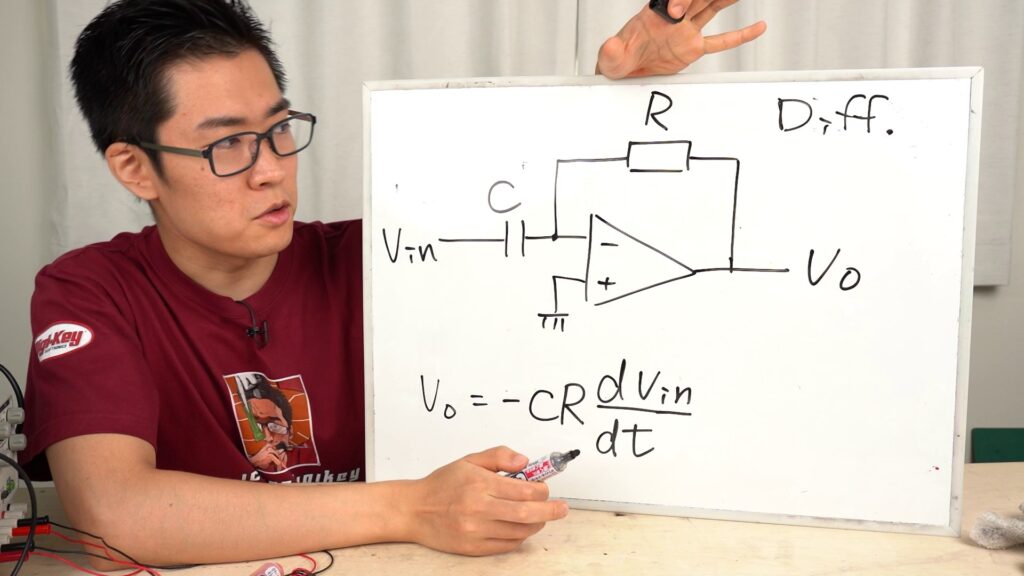
先程の積分回路で使っていたCとRの位置を逆にしたものです。これだけで実現できます。

ただしこの微分回路は、入力電圧に高周波のノイズが乗っていたりすると微分結果がその影響を受けてしまいます。ですので、電子式のアナログ計算機で微分回路が使われることはあまり無く、基本的には積分回路を使って微分方程式を解くことになります。

バネ – マス – ダンパモデルの数式

ここからは今回の本題である「ばねとおもりのモデル」を再現するための回路を設計していきます。

運動方程式

式(1)はバネ-マス-ダンパモデルの運動方程式です｡
Mをおもりの質量、Dを空気抵抗などによる減衰、Kをばね定数、gを重力加速度、yをバネの自然長からの重りの位置としました｡

式(2)は式(1)を加速度について整理したものです｡これで、式(1)を積分回路と加算回路の組み合わせで再現できるようになりました。

積分器で解く方法

次の図は式(2)を積分器を使ったブロック線図で表現したものです｡

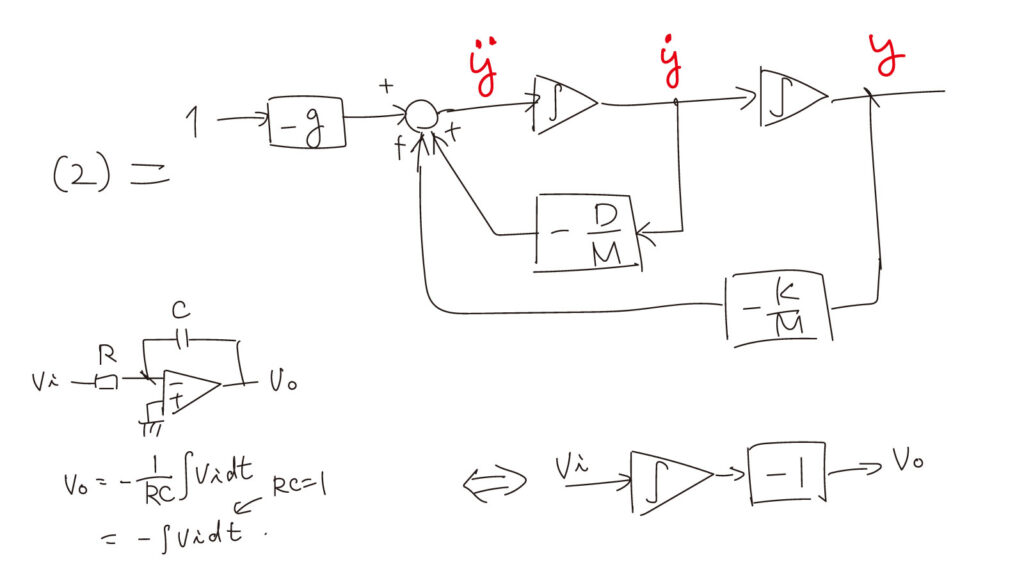
回路には2段の積分器があり、1段目の積分器は加算回路との組み合わせになっています。それぞれの入出力を加速度、速度、位置として、これに先ほどの運動方程式を当てはめます。

おもりを引っ張る重力加速度$-g$に加えて、速度、位置を表す電圧に、それぞれ減衰とばね定数を表す値をかけた値$-\frac{D}{M}\dot{y}$、$-\frac{K}{M}y$をそれぞれ加算して、第1段の積分器に入力してやればよいということになります。

次に積分器をオペアンプを使った積分回路に置き換えます｡

回路設計

ここからは先ほどの積分器を使ったブロック線図をオペアンプを使った積分回路と加算回路で実現していきます。
回路図は以下のようになります。

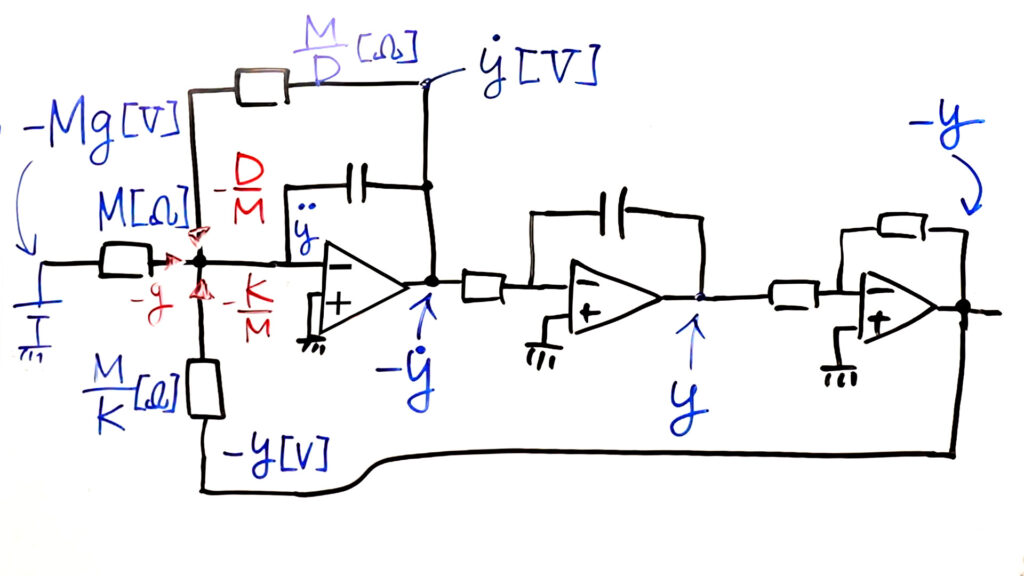
オペアンプを3つ使い、積分回路が2つと反転増幅回路が1つで構成されています。
ここで先ほどの運動方程式をもう一度見てみましょう。

$$\ddot{y}=-g-\frac{D}{M}\dot{y}-\frac{K}{M}y$$

この式と回路図がそれぞれどのように対応しているのか解説します。

重力加速度の入力

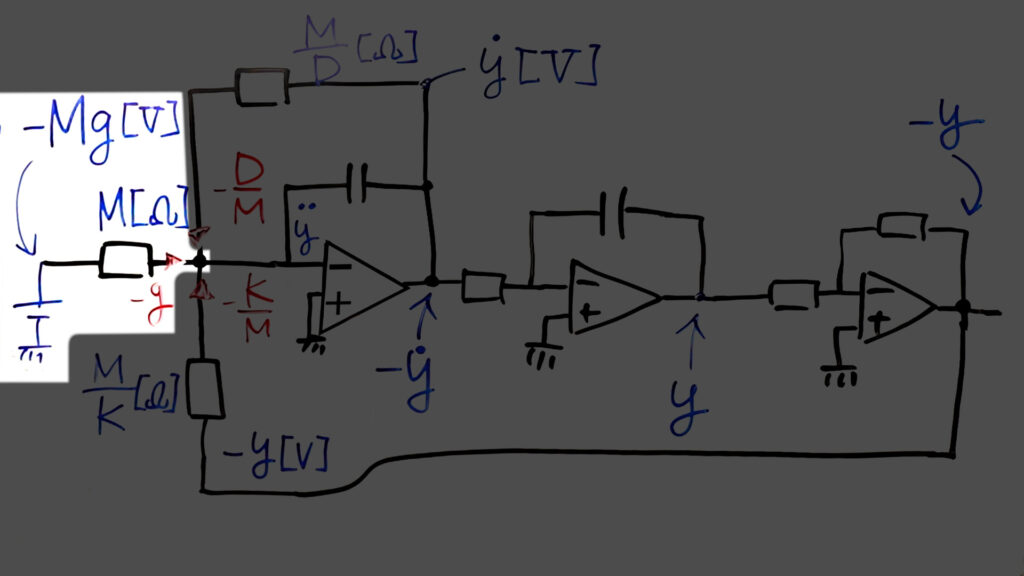
この回路では運動方程式で示した要素を加算して加速度としていますが、加算回路は電流で加算を行うため、電圧そのままでは計算ができません。そのため、方程式の中の-gの項については、おもりを重力方向に引く力-Mg[V]を電圧として与え、それを抵抗値M[Ω]で割ることで、下向きの重力加速度-g[A]を入力しています。

今回製作した回路では、質量Mを250[kΩ]の可変抵抗とし、シミュレーション開始のボタンを押すと-15[V]の電圧が入力されるようにしました。

入力電圧を変動させることで重力加速度-gも調整できるようにすることが可能ですが、今回は電圧は固定としました。もしそれを実装するのであれば、分圧抵抗では吸い込む電流によって電圧が変わってきてしまうため、間にボルテージフォロワなどを入れると良いでしょう。

減衰係数とばね定数の入力

$\ddot{y}$を積分した$-\dot{y}$[V]を$\frac{M}{D}$[Ω]で割った$-\frac{D}{M}\dot{y}$を、先ほどの-gと同様に1段目の積分器に入力します。$\frac{M}{D}$[Ω]は1[MΩ]の可変抵抗として調整できるようにしました。

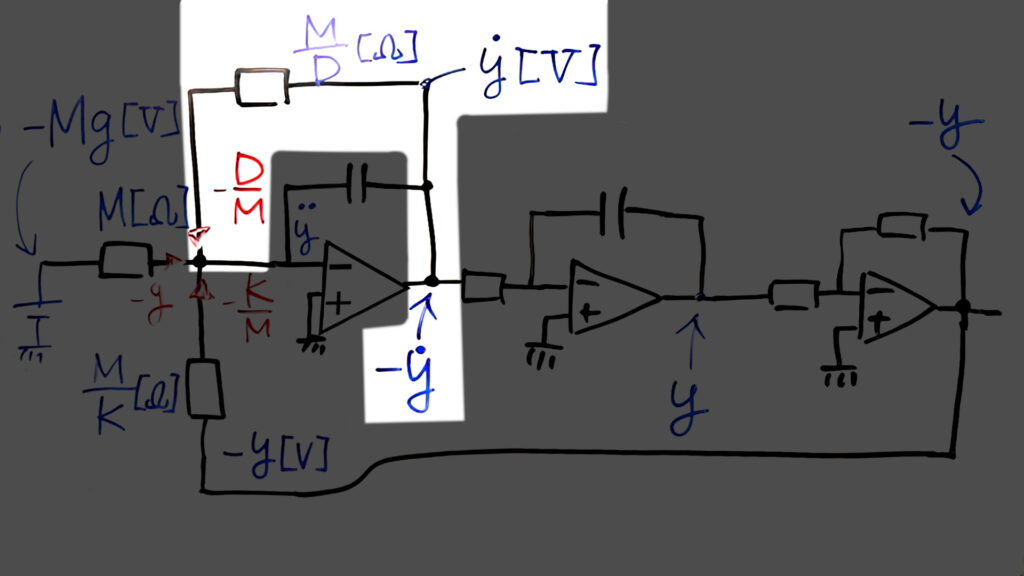
$-\frac{K}{M}y$についても同様です。

ただし、積分回路では入力電圧に対して積分結果が反転して出力されるため、入力の$\ddot{y}$に対して1段目の出力は$-\dot{y}$、また、それを入力された2段目の積分器の出力は${y}$になります。そのため、前章のブロック線図では省略していましたが、2段目の積分回路の後に1倍の反転増幅回路を置いて$-y$を出力しています。

その電圧から$\frac{M}{K}$[Ω]の抵抗値で割ることで、$-\frac{K}{M}y$[A]の電流を出力しています。可変抵抗は10kΩのものを使用しています。

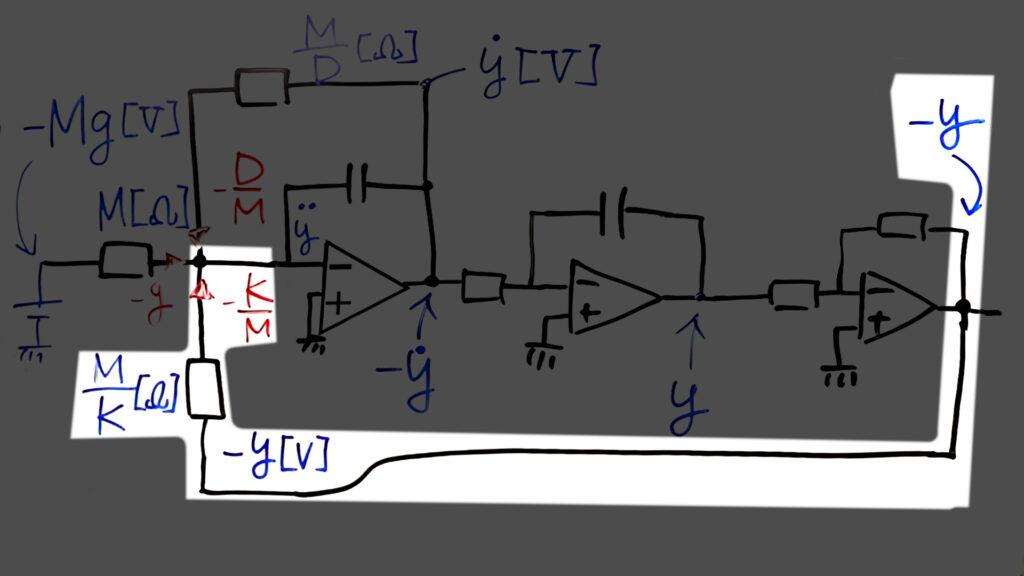
以上の要素をネガティブフィードバックとして1段目の入力に戻すことで、2段目の積分器の出力から減衰振動の波形が出力されます。

ソフトウェア上での回路シミュレーション

ここまでで、力学的な減衰振動モデルと電子回路がアナロジーな関係で再現可能であるということがわかってきました。

実際に電子回路に起こす前に、ソフトウェアシミュレーションで動作を確認してみます。

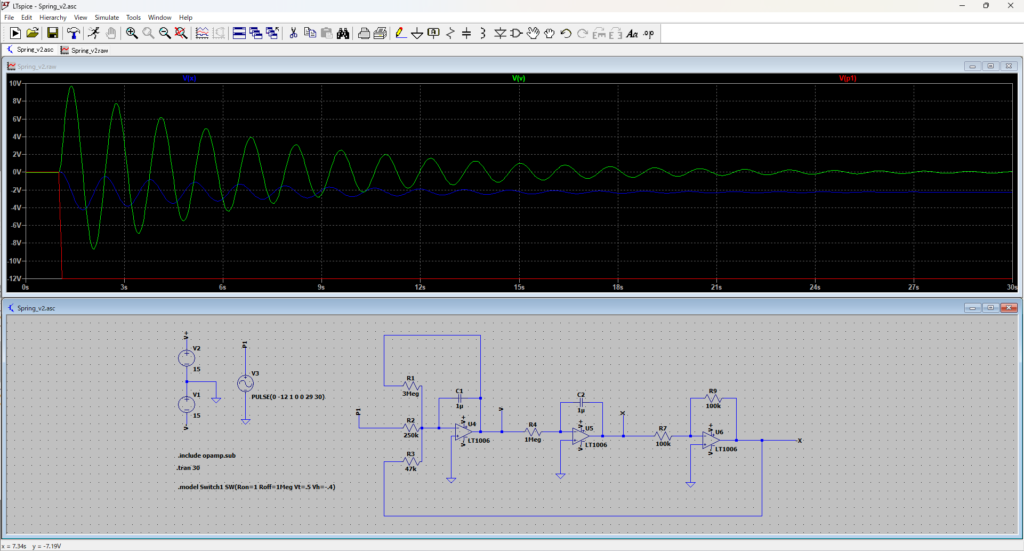
P1の電圧は-Mgを表し、シミュレーション開始1秒後に0Vから-12Vに変化します。つまり無負荷状態のばねに、いきなりおもりがぶら下がった状況を再現できます。

それぞれ位置と速度を表しているX, Vの波形を見てみると、おもりがぶら下がった瞬間に速度が立ち上がり、位置が下に振れて徐々に減衰していっていることがわかります。時間が経過すると速度は0で収束しますが、位置は-2V程度オフセットがかかった位置で収束しています。これがばねにおもりが吊るされた状態での釣り合いの位置です。

パラメータの設定によっては速度がオペアンプの出力電圧の上限や下限を超えて飽和してしまうため、抵抗値は要調整ですが、想定通りの動作をしていることがわかります。